201503 - page 122

北京工商大学学报( 社会科学版)摇 摇 摇 摇 2015 年摇 第 3 期
子(LM) 检验来选择采用空间滞后面板模型(SIP鄄
DM) 还是空间误差面板模型(SEPDM)。
三、 实证结果与分析
( 一 )Moran I 指数测算结果
选用经济距离空间权重矩阵 W 计算 Moran I
指数,图 1 显示了我国 30 个地区在 2000—2012
年农村居民消费水平 Moran I 指数变动情况 。 可
以发现, 各地区农村居民消费水平存在着正的空
间自相关性( 系数在 0郾 38 ~ 0郾 65 之间波动, 且均
通过了 5% 水平的显著性检验 ), 表明在样本期
内, 我国各地区农村居民消费水平在空间分布上
并不是随机的,而是随着其他地区消费水平的影
响, 在空间上表现出空间依赖性。
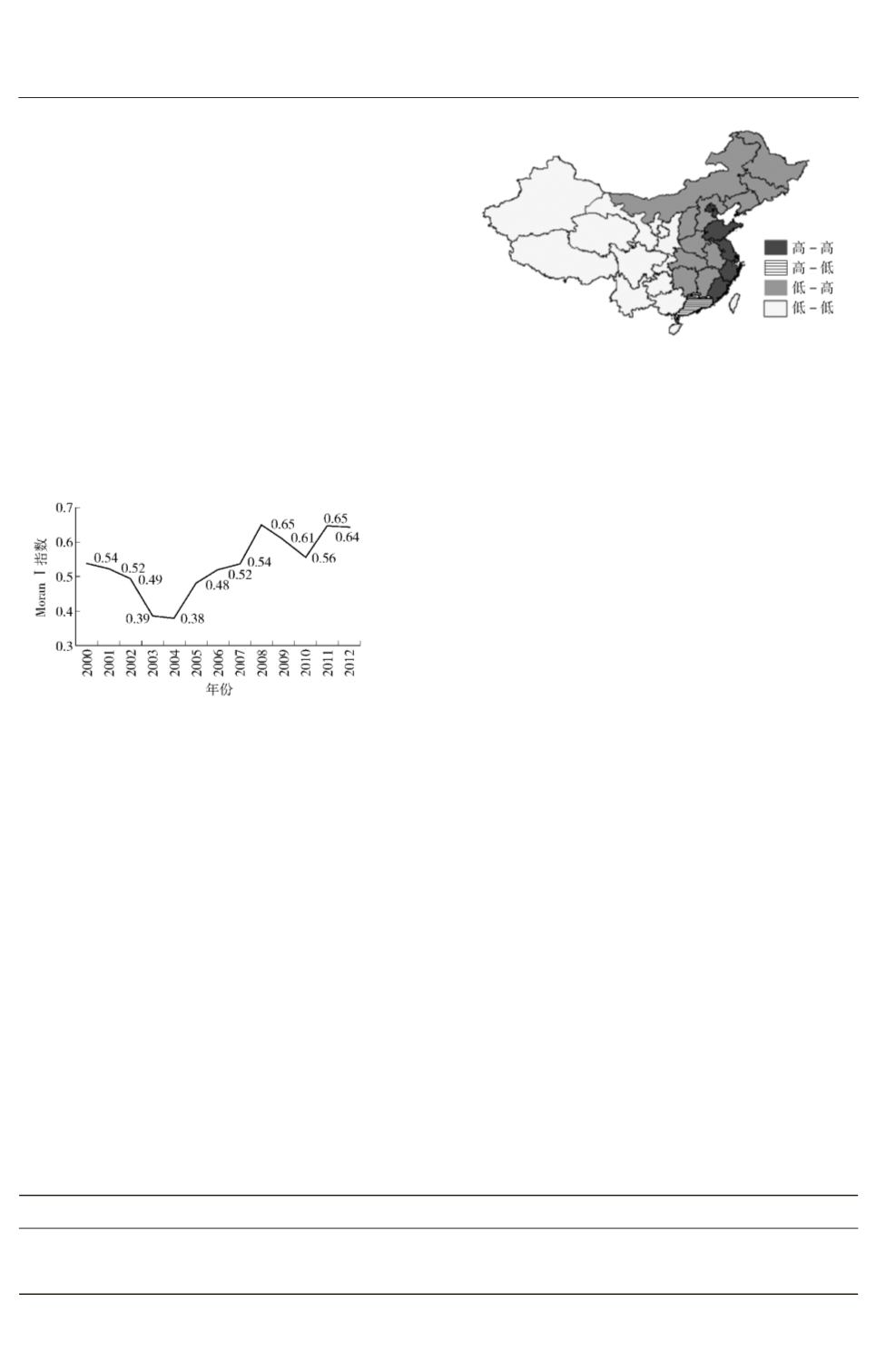
图 1摇 各地区农村居民消费水平 Moran I 指数及其变动
摇
为了进一步说明农村居民消费水平在空间分
布的局部特征,可以将 2012 年 Moran I 指数散点
图标识在地图上, 如图 2 所示。 由图 2 可以看到,
农村居民消费的地区分布规律十分明显,处于高 -
高和高 - 低区域的大都为东部沿海经济发达地
区, 而中西部地区则普遍处于低 - 高和低 - 低区
域。 这与经济发达地区农村居民消费水平要明显
高于欠发达地区的现实相符,反映出农村居民消
费水平具有空间依赖性和空间异质性。
( 二 ) 空间面板模型估计结果
在通过 Moran I 指数判定存在空间相关性的
基础上, 通过拉格朗日乘子(LM) 检验来选择采用
空间滞后面板模型(SIPDM)还是空间误差面板模
型(SEPDM)。 表 2 的结果显示,LM鄄err 统计值 >
摇 摇
图 2摇 2012 年农村居民消费水平 Moran I 指数散点图
摇 LM鄄lag 统计值, 这说明空间误差面板模型更优,
对于固定效应和随机效应的选择 ,通常而言,当样
本是随机从总体抽取时选择随机效应, 而当样本
是总体中一些特定个体时宜采用固定效应, 由于
研究的样本为 30 个地区, 并未满足随机原则, 因
此, 固定效应模型更为合适。 基于稳健性的需要,
实际估计过程中采取在主要解释变量为人口年龄
结构变量的基础上, 逐步加入收入水平、 财富水
平、 通胀波动和利率变动等控制变量的做法,为了
便于比较,本文还给出了普通面板模型的估计结
果。 表 3、表 4 和表 5 分别报告了普通面板模型、
静态和动态空间误差面板模型的估计结果 。
在逐步加入其余解释变量时, 表 3、表 4 和表
5 中“ 老龄化 冶 和 “ 少子化 冶 系数的符号和显著性
并未改变,其数值变动幅度也不大,表明估计结果
是稳健的。 进一步比较普通面板模型和空间面板
模型,由表 4 和表 5 的静态和动态空间面板模型
估计结果,表征农村居民消费水平空间依赖性的
空间相关系数 啄 ( W渍 的系数 ) 均为正值,且通过了
1% 的显著性水平检验, 印证了我国农村居民消费
水平在地区间存在着正向空间相关性, 即社会经
济特征相近的地区之间, 农村居民消费水平具有
互相促进的正影响。 忽略这种显著空间相关性的
干扰,则可能造成估计结果的偏误,表 3 普通面板
模型的估计结果中,“ 老龄化 冶 的估计系数明显小
于静态和动态空间面板模型的估计系数, 说明利
用传统的普通面板模型进行估计, 会造成 “ 老龄
摇 摇
表 2摇 模型的 LM 检验
检验方法 Lmerror R鄄Lmerror Lmlag R鄄Lmlag
统计值 21郾 182 21郾 039 10郾 205 9郾 063
p 值 0郾 000 0郾 000 0郾 000 0郾 000
·221·